以下是一些经常在深度学习中用到的函数。

logistic sigmoid 函数

logistic sigmoi函数的数学表达式为：$\phi(x)=\frac{1}{1+exp(-x)}$

函数的图像为：

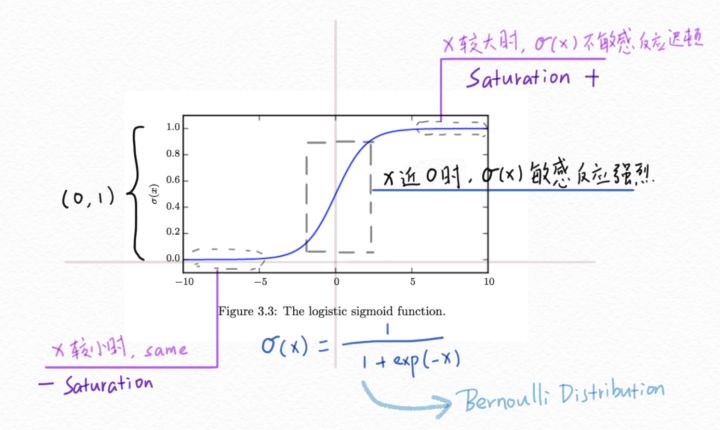
可以看出$\phi(x)$的值必然落在(0,1)之间，这就可以很好的用来生成伯努利分布的$\phi$。当x的绝对值非常大时，函数的变化变得不敏感，这称为饱和现象。

softplus 函数

softplus函数的数学表达式为：$\zeta(x)=log(1+exp(x))$

softplus函数的图像为：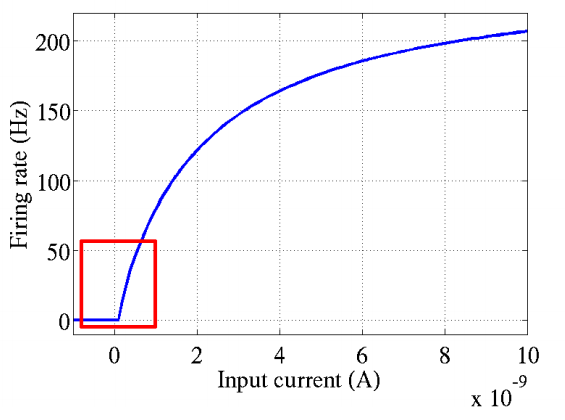

softplus函数常用来生成正态分布的方差的倒数$\beta=\frac{1}{\sigma^2}$。因为softplus函数的值正好位于(0,$\infty$)。

softmax 函数

在数学，尤其是概率论和相关领域中，Softmax函数，或称归一化指数函数，是逻辑函数的一种推广。它能将一个含任意实数的K维向量$\textrm{z}$“压缩”到另一个K维实向量$\sigma(\textrm{z})$中，使得每一个元素的范围都在${0,1}$之间，并且所有元素的和为1。该函数的形式通常按下面的式子给出：

$softmax(\textrm{x})i=\frac{exp(x_i)}{\sum\limits{j=1}^{n}exp(x_j)}$

也就是说，是该元素的指数与所有元素指数和的比值。

这个函数通常的意义：对向量进行归一化，凸显其中最大的值并抑制远低于最大值的其他分量。

END