深度学习入门1-线性代数-基本概念
理解标量、向量、矩阵、张量的含义和表达形式,目的是能理解含义,能读懂公式。
标量 scalar
一个标量是一个单独的数。通常表示为小写的英文字母,如:$x$,$s$。
向量 vector
一个向量是一列数。这些数是有序排列的。通过次序中的索引,可以确定每个单独的数。类似java中的数组。通常表示为粗体的小写英文字母,如:$\bf x$。
$x_1$是向量$\bf x$的第一个元素。当需要明确向量中的每一个元素时,可以使用方括号包围的一个纵列来表示,如:$\bf x \rm = \begin{bmatrix} x_1 \ x_2 \\vdots \x_n \end{bmatrix}$。有的时候需要明确的索引一个向量中的部分元素,可以先定义一个索引集合,再用索引集合做向量的下表,来表达。如:$s={1,3,6}$,然后写作$ \bf x_s$。可以通过补集的形式明确限定一组元素,如除了$x_1$之外的所有元素,表示为$\bf x_{-1}$。除了$x_1,x_3,x_6$之外的一个向量可以表示为$\bf x{-_s}$。
可以把向量看作空间上的一个点,向量中的每个元素相当于是每个坐标轴上的坐标。
矩阵 matrix
矩阵是一个二维数组,其中每个元素被两个索引确定。
矩阵通常用大写的粗体字母表示,如$\bf A$,该矩阵中第m行,第n列的元素表示为$A_{m,n}$。如果想表示整个第m行或者整个第n列,可以使用:表达,如$A_{m,:},A_{:,n}$。当需要明确表达矩阵中的元素时,可以使用以下形式表达:$\begin{bmatrix} A_{1,1} \quad A_{1,2} \ A_{2,1} \quad A_{2,2}\end{bmatrix}$。而$f(\bf A \rm )_{m,n}$ 表示函数$f$作用在矩阵$\bf A$上输出的第m行,第n个元素。
张量 tensor
张量是深度学习的核心概念之一,google的tensorflow框架的命名即来源于此。作为一个离开数学十几年的人,我花了一些时间去理解这个概念。
张量是一个这样的量,它能在不同的参考系中按照特定的法则进行变换。它的物理意义是使的物理公式的表达独立于参考系[^1]。
比如两个粒子1和2经过散射变成了3和4。
在a参考系中,能动量守恒是$(E_{a,1},P_{a,1})+(E_{a,2},P_{a,2})=(E_{a,3},P_{a,3})+(E_{a,4},P_{a,4})$
在b参考系中,能动量守恒是$(E_{b,1},P_{b,1})+(E_{b,2},P_{b,2})=(E_{b,3},P_{b,3})+(E_{b,4},P_{b,4})$
那么可以用张量表达为$T_1+T_2=T_3+T_4$
张量是多重线性函数,$T(v_1,v_2,\dots,v_r)$,输入r个向量,输出一个数,r称为张量的阶数。多重线性是指张量对于每个参数都是线性的[^2]。线性的本质是齐次性和可加性,也可以简单理解为张量与每个参数的关系函数,画成图像的话是一条直线。
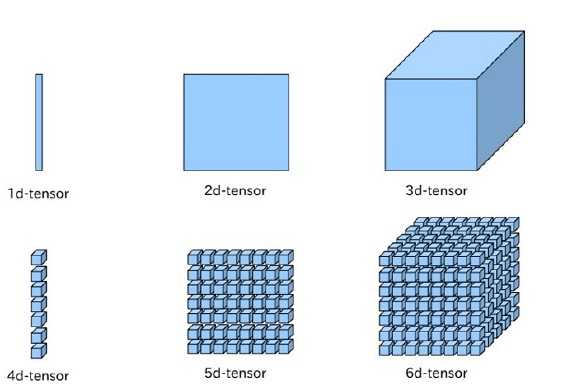
在机器学习领域,张量可以更简化的理解为N维数组。0阶张量就是标量,1阶张量就是向量,2阶张量就是矩阵,3阶及以上就没有特殊的称呼,直接称为N阶张量。下图来源于csdn[^3]。
END
[^1]: 知乎-andrew shen
[^2]: 知乎-郭诚
[^3]: 高维数组的机器学习
