什么是距离

在机器学习领域，距离是一个核心的概念，距离是用来衡量两个对象多近、多相似或者差别有多大的一个标尺。下面是近期学习过程中总结的对距离的理解。

闵科夫斯基距离

我们知道$3$比$2$大，那$3$为什么比$2$大呢？实际上我们假设了原点，$3-2$是$(3,0)$到$(0,0)$的距离减去$(2,0)$到$(0,0)$的距离。$(3,0)$到$(0,0)$的距离是$3$是显而易见的。但是是怎么算出来的呢？或者考虑不那么特殊的点，比如$(3,4)$这个点，它到$(0,0)$的距离是多远呢？这是个勾股定理问题。

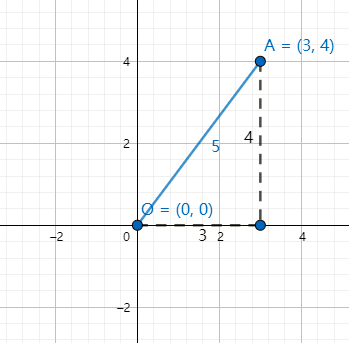
如上图所示，OA的距离是$\sqrt{(3-0)^2+(4-0)^2}=\sqrt{3^2+4^2}=5$

将上式再抽象一层，假设两点$P(x_1,x_2),Q(y_1,y_2)$，那么两点之间的距离为:

$\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}$

这样计算出来的距离即称为欧几里得距离。欧几里得距离的一个更通用表达如下:

$d(x,y)=\sqrt{\sum_{i=0}^n(x_i-y_i)^2}$

可以看到，在欧几里得距离里是将两个点的坐标对减的平方求和再开根号。将欧几里得距离推广，可以得到这样的一个距离表达式。

$d_p(x,y)=(\sum_{i=0}^n|x_i-y_i|^p)^\frac{1}{p}$

这个表达式称为闵科夫斯基距离。

当 $p=2$时，闵科夫斯基距离就是欧几里得距离。

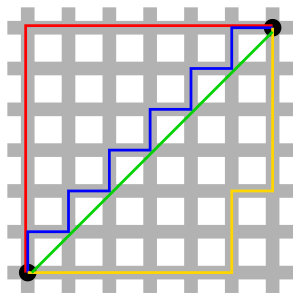
当$P=1$时，闵科夫斯基距离转变成$\sum_{i=0}^n|x_i-y_i|$，它的含义可以描述成两个坐标点在坐标系下的绝对轴距的总和。这称之为曼哈顿距离。下图是取自维基百科的一个示意图。假设图中两黑点之间只有灰色通路可行，那么很容易理解俩黑点的距离即为这两点间的曼哈顿距离。曼哈顿距离的实际应用价值，可以看一个例子。

当$P=\infty$时，闵科夫斯基距离转变成$max_{i=0}^n|x_i-y_i|$，即两个点的坐标差值的最大值。这称之为切比雪夫距离。

下图是距离原点的距离为5的点所得到的图形。最外层的正方形是切比雪夫距离为5，圆形是欧几里得距离为5，最内的正方形是曼哈顿距离为5。

余弦距离

现在有两个人，一个人身高1米8，一个人身高1米5，我们知道这两个人的差30厘米。那么考虑更多维度，如果A、B两个人，A(180,90)，B(170,60)，前者是身高后者是体重。那么这两个人差多少呢？或者说这两个人有多相似呢？这个时候就要引入另外一种距离，余弦距离。

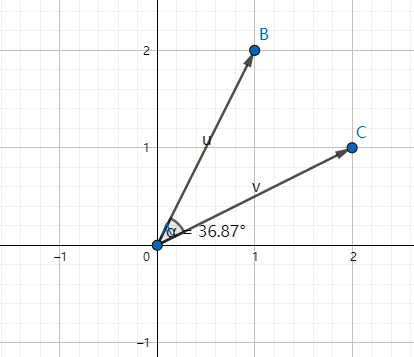
所谓$B$和$C$的余弦距离，就是$\vec {OB}，\vec {OC}$两个向量夹角的余弦值。计算公式如下：

$设x,y是两个向量，d(x,y)=\frac{x\bullet y}{||x||||y||}，即为向量的点积除以模的积。$

当夹角为0°时，余弦值为1，代表两个向量方向相同；

当夹角为90°时，余弦值为0，代表两个向量互相独立；

当夹角为180°时，余弦值为-1，代表两个向量方向相反；

余弦相似度在度量文本相似度、用户相似度、物品相似度的时候都较为常用。

比如有如下两个句子：

句子A：他不仅是一个歌手，还是一个舞者
句子B：他既是一个歌手，也是一个舞者

那么如何计算以上两个句子的相似度，首先我们要找到如何评价这两个句子，用什么方法将这两个句子向量化？我们最直观的看，两个句子用词相近，那句子整体相似度就高，因此我们从词频入手，来计算其相似性。

首先，进行分词处理：

句子A：他不仅是一个歌手还是一个舞者
句子B：他既是一个歌手也是一个舞者

其次，列出所有的词：

他不仅既是一个歌手还也舞者

第三步：计算词频

句子A：他（1）不仅（1）既（0）是（2）一个（2）歌手（1）还（1）也（0）舞（1）
句子B：他（1）不仅（0）既（1）是（2）一个（2）歌手（1）还（0）也（1）舞（1）

第四步：

我们总结出来两个句子的词频向量：

句子A(1,1,0,2,2,1,1,0,1)
句子B(1,0,1,2,2,1,0,1,1)

这样问题就变成了如何计算这两个向量的相似程度。都是从原点（[0, 0, …]）出发，指向不同的方向的向量。通过公式计算得出余弦距离为

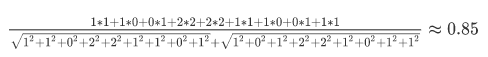
通过余弦相似度公式我们计算出来这来两句话意思很相近。

莱文斯坦距离

再考虑一个场景，现在有2个单词good和golden。允许你对good使用删除、添加、替换操作，那么经过多少次操作才能变成golden呢？

good->gold (o->l)
gold->golde (->e)
golde->golden (->n)

可见经过三次操作，完成了转换，那么3称之为莱文斯坦距离。莱文斯坦距离被应用在DNA分析、拼写检查、语音辨识、抄袭侦测等场景。

马哈拉诺比斯距离

前面说的距离都是在说两个个体之间的距离，现在将问题扩展到个体与群体之间。如下图：

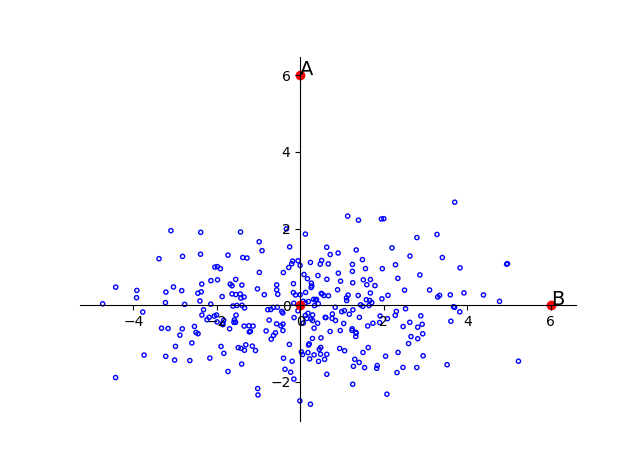
图中所有蓝色的点组成了一个群体G。那么A点离这个群体G的距离是多少呢？

很容易想到的是算出这个群体G的中间点O，然后计算AO之间的欧几里得距离，将这个距离作为A点离G的距离。那么在这种算法下，A点和B点离G有相同的距离。但我们从直观上知道B离G更近，为什么呢？

因为群体G在水平方向上的跨度比在垂直方向上的跨度更大。这个跨度就是标准差。所以我们不仅要考虑离中心点的距离还要衡量群体在对应方向上的变化范围。

我们将这个概念扩散到N维的情况下：

假设样本点为$\vec{x} = (x_1,x_2,\dots,x_N)^T$，数据集分布的均值是$\vec{\mu}= (\mu_1,\mu_2,\dots,\mu_N)^T$，协方差矩阵为$S$，那么这个样本点与数据集合的距离为

$D_M(\vec{x})=\sqrt{(\vec{x}-\vec\mu)^TS^{-1}(\vec{x}-\vec\mu)}$

这个距离称之为马哈拉诺比斯距离。

杰卡德距离

现在再考虑另一种情况，现在有集合$X$和$Y$。$X={1，2，3},Y={2,3,5}$，那么如何衡量这2个集合之间的相似性呢？很容易想到一种计算方法，就是用相同的元素个数除以总的元素个数。即：

$J(X,Y)=\frac{|X \cap Y|}{|X \cup Y|} = \frac{2}{4} = 0.5$

上式的值即称为杰卡德距离。它主要用来快速确定文本相似程度。